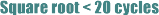
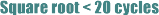 |    |
Brief
Integer squareroot approximation which executes in 16-27 cycles through effective bitsearch and 256 byte LUT table. Higer value for 486, lower for Pentium systems. On both CPU:s this means a performance improvement of at least 330% compared to using the FPU. In addition one removes the overhead of converting the integer value to a float and back again.
Observation
SQRT(2^16) = 2^8, SQRT(2^10) = 2^5. Interesting, just half the position of the bit. But what if we've got a multibit number such as 2710h (=10000 dec)?
Trial
Go looking for the bit in the highest position. The top bit in 2710h is nr 13. We shift the value to the right with 14 steps and put 14/2=>7 in some variable. 2710h shifted right 14 steps is 0.61035... if we take care of the decimal part. Now our value is in the interval 0..1. Let's do the SQRT on this value, for example using a LUT for this tiny interval. SQRT(0.61035...) => 0.78125. And now we use our old '7'. Shift the value 0.78125 to the left 7 times => 0.78125*2^7 = 100. Magic.
The reason to raise 13 to 14 is that we cannot shift 6.5 steps to the left in the end. We can actually turn this into an advantage rather than having to check for an odd number. We cut the highest bitsearch before the lowest bit is filled in.
Shame on Intel
BSR uses a bit by bit searching algorithm which wastes A LOT OF TIME. The 486 may use 100+ cycles for this, the 586 70+ cycles. During this time the squareroot algorithm here described will be done with at least four squareroots. Of course we use a binary search instead. Is the highest bit in the lower 16 bits ? YES: go search there. NO: search the upper 16 bits. Then, is the highest bit among the lower 8 bits or upper 8 bits? Then equally for 4 bits and 2 bits. In the squareroot algorithm we don't care about the last bit as explained above. So we're down to 4 CMP and 4 branch instructions which are taken 50% of the time. In the end we have to load the position in a register, all in all 9 instructions, which, according to Intel documentation executes in 9 clocks. This means on average an improvement with approx 340% compared to the Intel BSR instruction.
Note: This used to be true, but the AMD K6, Intel Pentium Pro and Intel Pentium II executes the BSR in about 2 cycles (if I have correct information). This would reduce the code size and speed up the code. Using BSR on the Intel CPUs is a must since a mispredicted branch may cost as much as 20 cycles.
Getting to the root of things
When we've found the highest bit we renember this value, with some modifications, to later. Then we consult the LUT for interval 0..1. After this we use the modified position value and shift the result left by this. Voila that's our square root!
How to modify the final shift value
We can choose which precision and where to have a decimal point in the 32 bit quantity. Below implementation uses no decimal point and a 8 bit precision LUT with 256 entries. Entry 'i' in the LUT represents SQRT(i/256). The precision of the LUT, which bit position the decimalpoint resides in the LUT and the decimal position on the numbers we operate on decide how to modify the highest bitposition number ( = how much to shift left in the end ). The number of times to shift left will be ( Position of highest bit / 2 ) + Constant. If this ends up negative right is the way to shift.
Below we end up having to shift right in 50% of the cases. This gives no execution penalty since we know this in the middle of the 'software BSR' sequence.
A final touch
We may further exploit the software version of the BSR instruction by eliminating a jump to a common code section to tidy up things. In this way we eliminate stack and register usage ( except EAX ) and get rid of a timeconsuming 'SHL EAX,CL' instruction plus a 'JMP' instruction. Now the algorithm seems more like splitting the incoming value in 16 cases by 4 tests. All shiftvalues are now coded into the instructions.
Performance
A 256 byte LUT is used. This could be reduced to 192 bytes since any of the top two bits must be one due to the shifting. But then we would have to take care of the ZERO case specially. Not worth it.
The algorithm is actually 'value = floor( sqrt(number) )' This is actually easy to modify to a correct rounding with a 1(2?) clocks penalty if the value in itself is important. In most cases this lack of rounding is not a problem.
On a 486 below 32 bit PM implementation executes in 27 cycles on a 486 including call/ret ( Timed for 30E6 squareroots ). In all cases the squareroot is found in 12 instructions. On a 586 this means a slightly higher number of clocks than instructions. Not timed.
On most numbers the error is below 0.75%. The accuracy for low numbers cannot be very good since 1.41.. which is the squarerot of 2 must be given the value 1 or 2, a 40% error. The error keeps dropping up to 16384, when the average error will be 0.4%. If a decimal point is used at bit 16 the low numbers aren't a problem anymore.
Implementation:
Below is C-Code to set up the LUT and the ASM code providing the function 'isqrt' (Integer Squareroot). This has been compiled under Watcom C but should be very easy to port. Watcom, for some odd reason, adds an underbar after the function name. The argument to the ASM function is passed in EAX and the result returned in EAX. The function is not suited for inline expansion since the it's size is approximately 200 bytes.
#include "stdio.h"
#include "math.h"
long isqrt( long nr );
unsigned char sqrt_tab[256];
void SetupSqrtTable(){
long i;
for(i=0;i<256;i++)
sqrt_tab[i] = 256.0 * sqrt( i/256.0 );
}
void main(){
long nr,i;
SetupSqrtTable();
printf("\nNegative number to quit :");
while(1){
printf("\nNumber => ");
scanf("%d",&nr);
if(nr<0) break;
printf("\nSqrt is %d", isqrt(nr));
}
}This is the assembler part:;
; square root
;
; input:
; eax = integer value to root
;
; output:
; eax = root ( only bits 15..0 may be ones. )
;
; destroys:
; flags
;
PROC isqrt_ NEAR
cmp eax,10000h
jb c_15_0
cmp eax,1000000h
jb c_23_16
; bit 31..24
cmp eax,10000000h
jb c_27_24
cmp eax,40000000h
jb c_29_28
shr eax,24
mov al, [_sqrt_tab+eax]
shl eax,8
ret
c_29_28:
shr eax,22
mov al, [_sqrt_tab+eax]
shl eax,7
ret
c_27_24:
cmp eax,4000000h
jb c_25_24
shr eax,20
mov al, [_sqrt_tab+eax]
shl eax,6
ret
c_25_24:
shr eax,18
mov al, [_sqrt_tab+eax]
shl eax,5
ret
; bit 23..16
c_23_16:
cmp eax,100000h
jb c_19_16
cmp eax,400000h
jb c_21_20
shr eax,16
mov al, [_sqrt_tab+eax]
shl eax,4
ret
c_21_20:
shr eax,14
mov al, [_sqrt_tab+eax]
shl eax,3
ret
c_19_16:
cmp eax,40000h
jb c_17_16
shr eax,12
mov al, [_sqrt_tab+eax]
shl eax,2
ret
c_17_16:
shr eax,10
mov al, [_sqrt_tab+eax]
shl eax,1
ret
c_15_0: cmp eax,100h
jb c_7_0
; bit 15..8
cmp eax,1000h
jb c_11_8
cmp eax,4000h
jb c_13_12
shr eax,8
mov al, [_sqrt_tab+eax]
ret
c_13_12:
shr eax,6
mov al, [_sqrt_tab+eax]
shr eax,1
ret
c_11_8: cmp eax,400h
jb c_9_8
shr eax,4
mov al, [_sqrt_tab+eax]
shr eax,2
ret
c_9_8: shr eax,2
mov al, [_sqrt_tab+eax]
shr eax,3
ret
;bit 7..0
c_7_0: cmp eax,10h
jb c_3_0
cmp eax,40h
jb c_5_4
mov al, [_sqrt_tab+eax]
shr eax,4
ret
c_5_4: shl eax,2
mov al, [_sqrt_tab+eax]
shr eax,5
ret
c_3_0: cmp eax,4h
jb c_1_0
shl eax,4
mov al, [_sqrt_tab+eax]
shr eax,6
ret
c_1_0: shl eax,6
mov al, [_sqrt_tab+eax]
shr eax,7
ret
ENDP isqrt_